Structures in the art

of Károly Ócsai

The most characteristic trait of the mature oeuvre of sculpture Károly Ócsai (1938-2011) can be considered his research into "crystal structures", and this was a defining feature of the last two decades of his life. Its immediate antecedents go back to the 1980s, but can only actually be understood, seen as an integral part of his early work, if we examine his experiments at the very beginning of the 1970s. The main aim of this essay is not then to give a detailed exposition of "crystal structure" research (this has already been done elsewhere), but to prove how strongly this is bound to the spread of structuralism and semiotics in the 1960s and 70s. 1

In the October 1972 number of the journal Művészet an article on the art of Károly Ócsai was published. The author Klára Soós recurrently emphasized the structural and geometric character of his sculptures, thus the basic characteristics of "crystal structures" can already be found in this article. The young artist described his endeavours as follows: "My aim is to unpack the content immanently arising from the elements and formal means I have fashioned myself," 2 and for sure, if we look at the works from 1972 (and some from 1971) we see that the works organize themselves out of organic abstract elements into forms and figures.

A group of sketch drawings seems to show this method of creation: they were made by cutting out abstract elements, pasting them together, redrawing them and hatching them, as if they were parts of a set of building blocks.

[1] Gábor Andrási: The Seventies. In: Andrási Gabor - Gabor Pataki - Gyorgy Szucs - Zwickl Andras: Hungary
75/5000 fine art in the 20th century. Corvina, Budapest, 1999, 181-209. (193-194.)

[2] Klára Soós: On the Sculpture of Károly Ócsai, Art, September 1972 XIII. Vol. 9.sz. 22-23. (23)

In his sculptures entitled The Column and Maneken, the artist has gone one step further, creating them with essentially identical but rotated components.

At around the same time the above article was published, (between the commission, 7 June 1972, and the presentation, on 24 October), he used a similar method to make the design for a wall cladding surrounding a relief depicting the man after whom the Ervin Baktay Grammar School in Dunaharaszti was named; he probably considered the cladding a more essential part of his work than the commission for a realist portrait.

According to the minutes taken by the jury when the design was presented "every member of the jury finds the aesthetic thinking behind the artist's design, in which the sculptor has endeavoured to convey the thinking of Indian architecture, extremely worthy". These practically contemporary quotations from the article in Művészet and the minutes show that at one and the same time (and obviously from two different aspects of the same idea) Károly Ócsai experimented with the unpacking of content immanently arising from formal elements, and with the opportunity of the visual mapping of some pre-defined (abstracted) intellectual content.

On the basis of these, other notes containing not only sketches but only conceptual tables can be interpreted.

Károly Ócsai attempted here to couple one tangible characteristic or quality to the most fundamental, general and special concepts. As he himself wrote: “In terms of themes, I am aided by an idea in Marxist aesthetics, the idea that one of the main functions of art is to anthropomorphize the environment, and nature, extending this idea to everything that can be grasped through observation, or translated into a visual language (e.g. scientific concepts).”.
To put it more accurately, as can be seen from the tabular form, he assigned the intersections of the concepts to aesthetic qualities, and to tangible sculptural characteristics that match with them; in Klára Soós's words: "He generally strives for multifaceted similarities. He would like these to develop into a succinct metaphor and the new concept to stand for itself so that only the emotional charge of the elements remains, and they can suggest independent associations."

To make the idea quite clear: the tabular form, represented in a plane, is only an approximation to what the artist was thinking, because only concepts of the same nature were assigned to any one plane, and planes of different categories of concepts created a kind of system cutting through space. The artist made similar notes over a period spanning a quarter of a century, over which the concept obviously changed, and unfortunately only in the rarest of cases is it expressed in such a way as to be clearly understood by the public at large. One of his sketches, for instance, suggests that the conceptual mesh is formed along the vertices, edges, and planes of two tetrahedrons that can be inscribed into a hexahedron (a cube), and the octahedron produced at their intersection, while in a lecture he stated: "Concepts, giving up their linear nature, lay in the plane, revealing the multiplicity of their relationships, and described a twelve-pointed magic Mandala radiating from within” then later "And this is now the third dimension, the virtual appearance of the perfect Platonic body, the icosahedron; the logical connection of art, particularly sculpture, to the Universe."

Károly Ócsai aimed to do nothing less than create a universal code system with which the visual characteristics of a work of sculpture can be simply transcribed to the language of universal concepts. To simplify things somewhat: one can write "Indian architecture and thinking" into the correct place, and on the other side a "matching" sculptural form appears; or vice versa: one can insert the elements or formal "tools" one has created, and the conceptual content to which they correspond (“immanently arising from them”) will unfold.

3 Submission for the Derkovits scholarship, 10 March 1971 (in the artist's estate).
The humanization of the environment crops up later in the artist's choice of words, for instance when making his first "crystalline structure" work the Saturnalia, see Károly Bebesi: Humanizálni a teret. Ócsai Károly szobrai.
művének, a Szaturnáliának a készítésekor, ld.
The sculptures of Károly Ócsai). Dunántúli Napló, 1st August 1982.
4 Klára Soós op. cit. 23.
The Four Elements Symposium of the Fourth International Sculpture Drawing Biennale. Budapest, 29 March 1996, 78-85.

An entrancing idea, and a heroic undertaking, which Károly Ócsai was however not able to complete. Even his notes show that he believed the concepts could be organized or classified in several different ways, so even devising one side of the code system would have been an enormous intellectual accomplishment. We can however be almost sure that the artist constantly applied his half-finished, changing ideas in his own practical creative work as an artist, either when he had to find the most suitable visual form for a given theme, or when, forging ahead on his own path, he sought the inner structure of a work of art. The originality of the idea can hardly be emphasized enough, even if precedents can be found in those eras of human culture that strive for universalism, such as in scholastic philosophy (particularly in the work of Raymundus Lullus) or in the Baroque (Iconologia), and even the iconic artists of abstraction, Malevich and Kandinsky. But we can see how this idea is particularly relevant in the age of computing, looking back at its beginnings. For Károly Ócsai's generation, the spread of structuralism and semiotics in the 1960s and 70s in Hungary was a defining experience; this same endeavour in systems theory and semiotics was expressed in the artist's thinking.

Structuralism and semiotics are related, closely interconnected systems, and they belong closely together in Ócsai's thinking too, yet it would be expedient to tend towards some simplification and separate these components in his work. The system presented above, which (despite its marked structuredness) can be said to be "semiotic" cannot be firmly "grasped" by an everyday observer or even art historian in the development of his career, which (in spite of its semiotic aspects) can rather be traced in its structural framework and the way this framework developed.

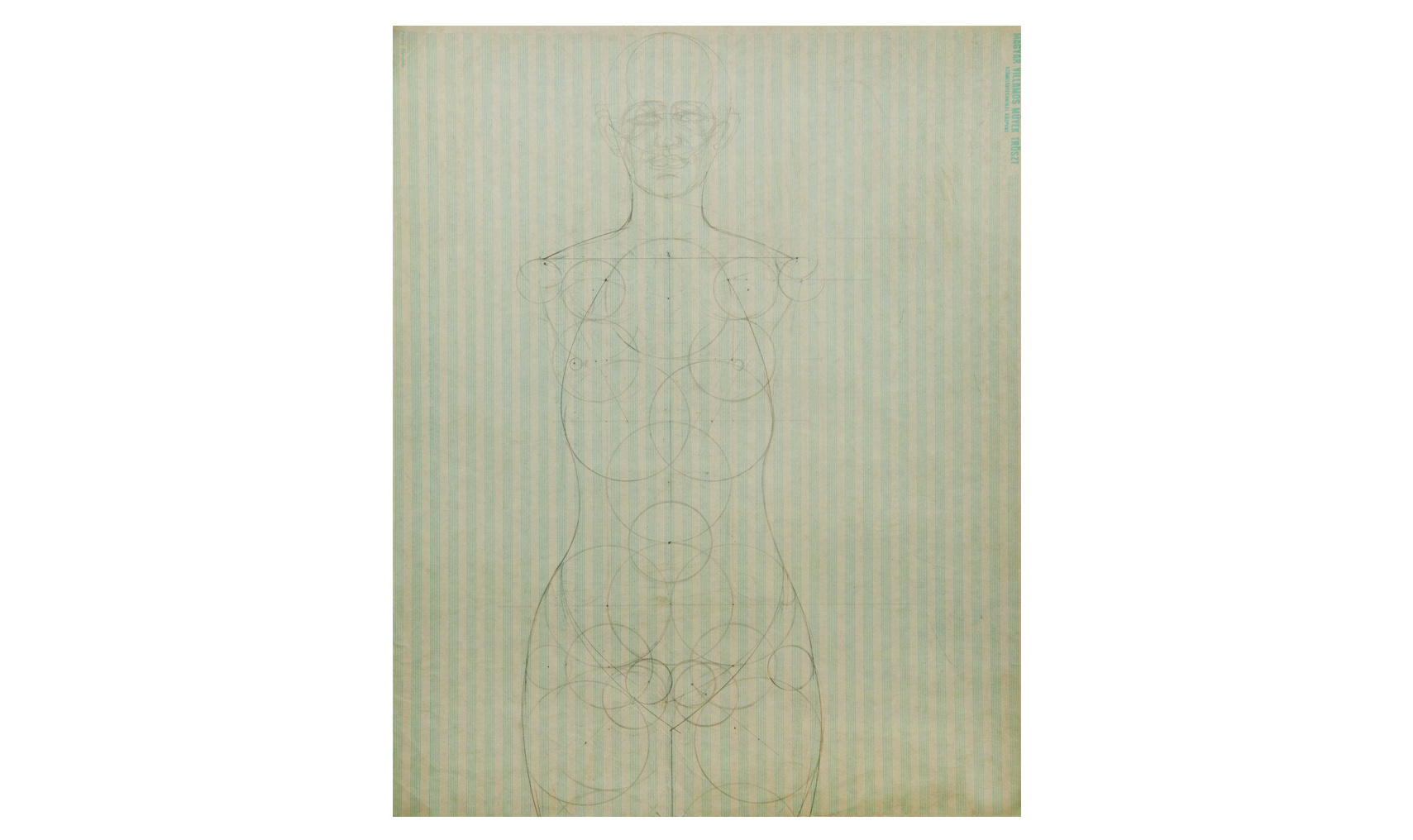
As we mentioned above, in about 1972 Károly Ócsai believed his sculptures (which appear as abstracted organic figures) could be constructed on the basis of the organization of (organic) abstract elements he had created himself. However, the elements that even in their form demonstrate organic existence, from time to time cede their place to geometric forms. The sculpture Mannequin (1972), already mentioned, is made of the rotated repetitions of a hyperboloid form. Here beyond doubt the semiotic content of the form correlates to the hollowed, formal meaning of the "mannequin" – a tailor's dummy. In this context it is interesting that for the heads planned for the mannequins of an exhibition, Ócsai represented the reduced form in parallel vertical planes (on sheets of plexiglass) already in summer 1971.

The date is assured by a comment ascribed by the artist to Gyula Pauer, in relation to the following exhibition:

Sechs Ungarische Künstler zum ersten mal in Wien (Imre Bak, János Fajó, Tamás Hencze, István Nádler, Gyula Pauer, Gábor Tót), Vienna, 14.06.1971 Galerie im Griechenbeisl, see

http://www.basis-wien.at/db/object/111783;jsessionid=9CDD03019C2DD2A37C45BAA535A676FB

The six sketches in which Károly Ócsai deconstructs the human form into vertically divided planes would be difficult to place elsewhere in his oeuvre. Interestingly, in these drawings, the vertical sections are also simplified into geometric planes. However, these sketches, the like of which is found nowhere else in the oeuvre, can naturally also be considered an isolated experiment.

But it is certain that when decades later the artist returned to the subject of the "dummy" (in 1987, in response to a commission), he similarly felt the geometric, somewhat "contrived" structure of the figure to be the primary one, because he formed it exclusively from a system of spheres made of various diameters. This work represents an extremely original theoretical and practical contribution to the series of attempts to canonize the ideal human body according to fixed rations (e.g. Dürer).

Over his career Károly Ócsai did not depart from organic forms (even the arcs of spheres and hyperboloids give this impression); what can have led him then to bodies such as the tetrahedron and the octahedron, so dry and alien to natural forms as they are? The artist later explained this by saying that in the "crystal structure" he had discovered an analogy for organic growth, but he may have felt his earlier great subject, "mitosis" (the division of cells) was much more relevant. When he spoke of his first work (Saturnalia) using a system of tetrahedra and octahedra, he stated: "here I tried out something that has been occupying me since 1973." So the artist himself places the genesis of the idea much earlier, to the early 1970s.

[7] Károly Bebesi: Humanizing the Space. The statues of Károly Ócsai. Transdanubian Journal, August 1982 First

But what can have happened in that year, to have such a determining influence on the entire later oeuvre? In 1973 Károly Ócsai was invited to an international mason's symposium (a creative seminar) in Prilep in Macedonia. It was obviously important for him to be able at last to carve in stone, on a monumental scale, one of his earlier sculpture designs, the Mannequin mentioned above. Károly Ócsai had learned the craft of carving in stone in the decorative sculptor Studio of the Art Contractor's Company (1960-64, the Képzőművészeti Kivitelező Vállalat), but until then he had always made his sculptures by modelling alone. It may have been while carving his first monumental stone sculpture that he had the idea that when making a monumental sculpture during the design phase one should take account not only of organic organization, but also of the crystal structure of the raw material which influences the realization of the artwork. This is pure speculation, but evidence for it is to be found in the artworks of the works of the years 1973-74, much more concise than hitherto, and in the sketches made for them a kind of geometrical network of lines appears for the first time.

Why, of the many forms of geometrizing, he should chose the tetrahedral-octahedral one in particular, is explained in an essay he wrote in 1989 entitled Architektonikus gondolkodás ma ("Architectonic thinking today"): “...I was looking for a crystal module structure, which if possible would approach the form encasing the sculpture, from which an objectified space could be constructed: and at once I wanted to overreach this and move towards organic form.” and: “I began to research non-right-angled geometric systems with which space can be filled completely." The deciding factor in the decision must thus have been the following properties: it most nearly approaching the organic form, and the way that it fills space entirely.

Károly Ócsai's research into "crystalling structures" can be divided into three phases that largely match different decades:
1980s: tetrahedral-octahedral system
1990s: compositions formed of mixed elements derived from the division of the tetrahedron
2000s: compositions formed from prismatic elements derived from the division of the tetrahedron

His experiments in the 1980s can be divided further into phases. The first period falls in the first half of the decade. Strangely, his first works are not sculptures in the strict sense, but rather architectural creations (a table to sit round, well fixtures, and pools), so they do not even approach organic forms; moreover, in line with this the elements they are constructed from are the size of bricks, so their trait of completely filling space is not apparent.

In all likelihood Károly Ócsai himself also realized that this path was a dead end, and only three such works by him are known. Similarly, three works are known on another subject (about which more later), and then there is no trace of research into crystalline structures until 1989. Presumably the artist felt the whole idea to be a dead end, and compared to the basic forms he had developed himself earlier these bodies obeying strict geometric laws must have seemed crude to him (evidence for this is that at this time he was mostly occupied with recreating of his works made at the beginning of the 1970s: he cast at least two of his previous works in bronze, he made two in ceramic, in human size, and managed to have one large-scale work erected in a public space).

The subject of the other three sculptures is chess. There is a relief from this period in which due to the perspective the squares on the chessboard are distorted into rhombuses, and this may have given the idea to use octahedra.

From there same period there is a small series of graphics in which there appear torsos and classical architectural elements (sometimes distinctly reminiscent of chess figures).

This is probably the series that the artist exhibited in 1989 with the title Atlantisz, and which bears a strong resemblance to the sculpture groups made between 1989 and 1992, including one group which bears a similar title. After a hiatus of half a decade Károly Ócsai once more took up the tetrahedral-octahedral system, but now he used the elements not as the building blocks for sculptures, but as forms in which to encase them. This solution is actually an effective twist of the opinion of which Lajos Németh wrote: "In European and thus in Hungarian sculpture, the cubic interpretation of space became dominant, thus essentially the principle of classical Greek sculpture, in which contrappposto motion takes place within cubic enclosed space, the composition is closed in a microcosm." In Greek sculptures we do not see this encasing cube, and neither do we see the encasing tetrahedral-octahedral structure in the sculptures Károly Ócsai made at this time. This can only be seen in the sketches, and in the fact that because of the rules of tessolation of the geometrical elements, every sculpture leans to the diagonal.

At the end of this extremely productive period it was precisely this latter characteristic that made Károly Ócsai dissatisfied with the entire system. His belief was that "a sculpture should stand on its pedestal". For a short while he left off with these experiments again, and tried to return to the right-angled coordinate system, using the traditional Cézannesque forms (the sphere, the cylinder, the cone) for compositions, and this probably led him to think through the problem systematically, eventually arriving at the solution.

If the typical basic elements of the right-angled coordinate system (i.e. the cubic/hexahedral space in which the basic directions lie at 90° to one another, and the basic unit is a natural number) are spheres, cylinders, and cones, from which everything can be constructed, then we can create the basic elements of a tetrahedral space (in which the basic directions lie at 60°, and the basic unit is a square root , and this can obviously be done by dividing, or "slicing up" the tetrahedron. Compared to the "ready" tetrahedron and octahedron, these forms were Károly Ócsai's "own", as he had said at the beginning of the 1970s. These were the elements the artist used to construct his compositions in the 1990s. In one of these sculpture designs we can also see how the organic form is latent behind the geometric frame.

8 Lajos Németh: Schaár Erzsébet szobrai a Műcsarnokban. [The Sculptures of Erzsébet Schaár in the Műcsarnok]. Kritika, 1970. No. 8, 1-3.
9 Because the tetrahedron can be derived from the diagonals of a square, the length of these edges are square roots (in the case of a square with sides measuring one unit, the diagonal is √2).

Thus a completely logical coherent system was born, which Károly Ócsai considered valid to the end of his life (as proven by the fact that even in the 2000s he created some works on this basis), yet at the threshold of the 2000s he developed an even more brilliant, more sophisticated version.

In a text for a 2006 competition (for a wall decoration in Corvinus University) he writes of the system: “...it changes from the right-angled coordinate system to a cosmic yet organic geometric system, where instead of 90 degrees there are 60, instead of hexahedra there are tetrahedra, instead of integers there are roots, and this too creates a new almost completely stereometric world.” “...it consists of a system of prisms delimited by more than 120 planes based on equilateral triangles, in effect pointing to the centre of a sphere. The variety of these prisms is expressed through their length (roots of integers 1-21), the width of the surfaces, and the variety of the inter-edge and interfacial angles, the whole creating a space-like, optical effect.”

Later the artist altered this method of division by reducing it to only 30 elements, and the edges of the prisms were simplified by being made parallel. This latter simplification can presumably be explained as a perspective interpretation of the elements pointing to the centre of the sphere (taking them to be parallel elements meeting at the vanishing point of the visible universe, on the basis of the "cosmic" expression above). The irrational element, the way the basic tactile element of the work is related to the perspective (optical) spectacle, appeared as we have seen in the relationship between the chess relief of the 1980s and the chess sculpture. The tetrahedral space of the system of the 1990s almost obviously offers the possibility of comparing the notion of a perspective cone or pyramid, and a triangular pyramid forming space (i.e. a tetrahedron). In the system of the 2000s it is highly likely the artist completed the irrational identification of tactile and optical space, otherwise we would have to leave the properties mentioned unjustified and unexplained. Unfortunately however Károly Ócsai did not note this down anywhere.

To sum up the most original aspect of his oeuvre, the research into crystal structures, can be divided into four separate periods that build one on the other (the present writer’s reconstruction):
1. the tetrahedron-octahedron system, as elements forming the mass of a work of art (1981-85)
2. the tetrahedron-otcahedron system as the space encompassing the artwork, as an alternative to the hexahedron (cube) (1988-1992
3. the tetrahedron as tangible space whose basic elements can be made from this (1994-99)
4. the tetrahedron as absolute space (both tangible and optic space) (1999-2011

10 The system continues to conceal irrational elements. The set of elements pointing to the centre of the sphere and also the set of elements of two (interpenetrating) tetrahedrea inscribed into one cube (one hexahedron).

Gábor Tokai

art historian